La función cosecante (abreviado como csc o cosec) es la razón trigonométrica recíproca de la función seno, o también su inverso multiplicativo:

csc ⁡ α = 1 sin ⁡ α = c a {\displaystyle \csc \alpha ={\frac {1}{\sin \alpha }}={\frac {c}{a}}}

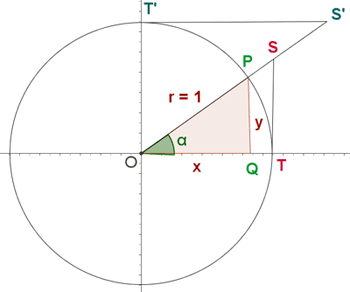
Forma geométrica

Sabiendo que:

csc ⁡ α = 1 sin α {\displaystyle \csc \alpha ={\frac {1}{\sin \;\alpha }}}

Trazando una recta horizontal que pasa por F que corta a r en G. A la vista de la figura, podemos ver que el ángulo de G es igual al ángulo de A, dado el triángulo GAF rectángulo en F:

csc ⁡ α = 1 sin α = A B ¯ C B ¯ = A G ¯ A F ¯ = A G ¯ 1 = A G ¯ {\displaystyle \csc \alpha ={\frac {1}{\sin \;\alpha }}={\frac {\overline {AB}}{\overline {CB}}}={\frac {\overline {AG}}{\overline {AF}}}={\frac {\overline {AG}}{1}}={\overline {AG}}}

Otra forma de obtener la representación geométrica es trazando la perpendicular a r por el punto B, esta perpendicular corta el eje y en K, con lo que tenemos:

csc ⁡ α = 1 sin α = A K ¯ A B ¯ = A K ¯ 1 = A K ¯ {\displaystyle \csc \alpha ={\frac {1}{\sin \;\alpha }}={\frac {\overline {AK}}{\overline {AB}}}={\frac {\overline {AK}}{1}}={\overline {AK}}}

Siendo una representación distinta de la anterior.

Representación gráfica

Seno y cosecante de un ángulo

Partiendo de la definición de cosecante como la inversa del seno:

csc ⁡ α = 1 sin ⁡ α {\displaystyle \csc \alpha ={\frac {1}{\sin \alpha }}}

Y conociendo la función seno previamente, podemos ver que para los valores en los que el seno vale cero, la cosecante se hace infinito, si la función seno tiende a cero desde valores negativos la cosecante tiende a: − ∞ {\displaystyle -\infty } .

lim α → 0 − sin ⁡ ( α ) = 0 − {\displaystyle \lim _{\alpha \to 0^{-}}\sin(\alpha )=0^{-}}
lim α → 0 − csc ⁡ ( α ) = 1 lim α → 0 − sin ⁡ ( α ) = 1 0 − = − ∞ {\displaystyle \lim _{\alpha \to 0^{-}}\csc(\alpha )={\cfrac {1}{{\underset {\alpha \to 0^{-}}{\lim }}\;\sin(\alpha )}}={\cfrac {1}{0^{-}}}=-\infty }

mientras que cuando el seno tiende a cero desde valores positivos la cosecante tiende a: ∞ {\displaystyle \infty } .

lim α → 0 sin ⁡ ( α ) = 0 {\displaystyle \lim _{\alpha \to 0^{ }}\sin(\alpha )=0^{ }}
lim α → 0 csc ⁡ ( α ) = 1 lim α → 0 sin ⁡ ( α ) = 1 0 = ∞ {\displaystyle \lim _{\alpha \to 0^{ }}\csc(\alpha )={\cfrac {1}{{\underset {\alpha \to 0^{ }}{\lim }}\;\sin(\alpha )}}={\cfrac {1}{0^{ }}}= \infty }

Cuando el seno del ángulo vale uno, su cosecante también vale uno, como se puede ver en la gráfica.

Véase también

  • Trigonometría
  • Identidad trigonométrica


Referencias

Bibliografía

  1. Cobo Mérida, Purificación (9 de 2008). Trigonometría, 4 ESO. Materiales Didácticos Bemal. ISBN 978-84-612-6049-2. 
  2. Cortés Espinosa de los Monteros, Nuria (2 de 2008). Actividades para unidad didáctica sobre trigonometría. Ediciones Didácticas y Pedagógicas S.L. ISBN 978-84-936336-3-9. «1 CD-ROM». 
  3. Merlini Navarro, Irene (2 de 2008). Trigonometría plana: tu material didáctico (1ª edición). Visión Libros. ISBN 978-84-9821-279-2. «1 CD-ROM». 

Enlaces externos

  • Weisstein, Eric W. «Cosecante». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
  • Matemática - Trigonometría




cosecante Diccionario de Matemáticas Superprof

Función cosecante Funciones

Cosecante

Cosecante

Cosecante